最新工作:

|
Deterministic Distribution of Multipartite Entanglement and Steering in a Quantum Network by Separable States
Meihong Wang, Yu Xiang, Haijun Kang, Dongmei Han, Yang Liu, Qiongyi He, Qihuang Gong, Xiaolong Su , and Kunchi Peng
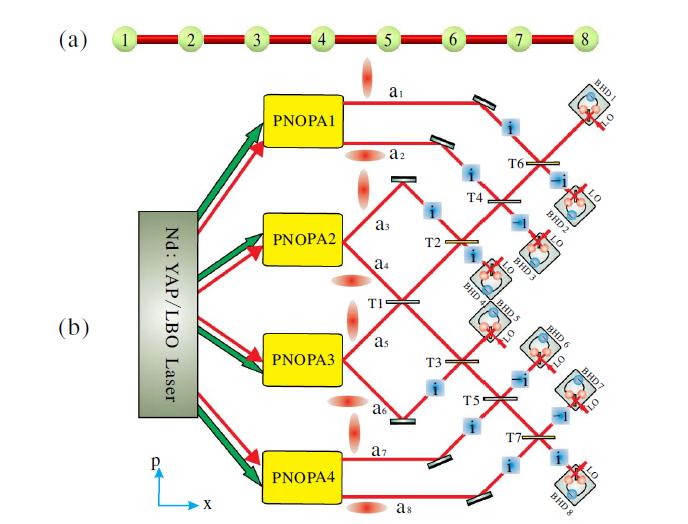
As two valuable quantum resources, Einstein-Podolsky-Rosen entanglement and steering play important roles in quantum-enhanced communication protocols. Distributing such quantum resources among multiple remote users in a network is a crucial precondition underlying various quantum tasks. We experimentally demonstrate the deterministic distribution of two- and three-mode Gaussian entanglement and steering by transmitting separable states in a network consisting of a quantum server and multiple users. In our experiment, entangled states are not prepared solely by the quantum server, but are created
among independent users during the distribution process. More specifically, the quantum server prepares separable squeezed states and applies classical displacements on them before spreading out, and users simply perform local beam-splitter operations and homodyne measurements after they receive separable states.We show that the distributed Gaussian entanglement and steerability are robust against channel loss. Furthermore, one-way Gaussian steering is achieved among users that is useful for further directional or highly asymmetric quantum information processing.
Phys. Rev. Lett. 125, 260506 (2020) PDF
|

|
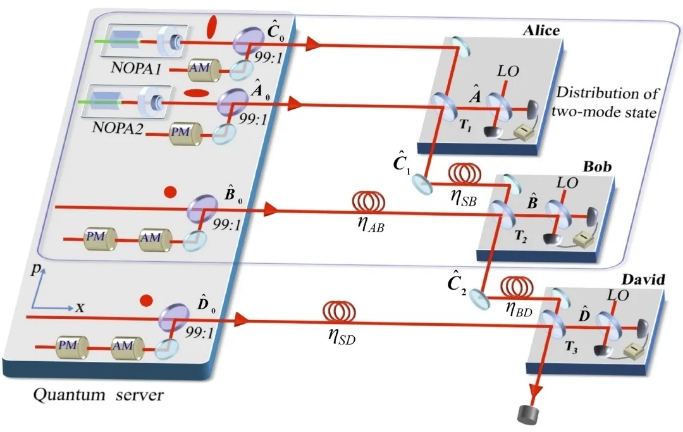
Experimental test of error-tradeoff uncertainty relation using a continuous-variable entangled state
Yang Liu, Zhihao Ma, Haijun Kang, Dongmei Han, Meihong Wang, Zhongzhong Qin, Xiaolong Su, and Kunchi Peng
Heisenberg’s original uncertainty relation is related to measurement effect, which is different from the preparation uncertainty relation. However, it has been shown that Heisenberg’s error disturbance uncertainty relation is not valid in some cases. We experimentally test the error-tradeoff uncertainty relation by using a continuous-variable Gaussian Einstein–Podolsky–Rosen (EPR)-entangled state. Based on the quantum correlation between the two entangled optical beams, the errors on amplitude and phase quadratures of one EPR optical beam coming from joint measurement are estimated, respectively, which are used to verify the error–tradeoff relation. Especially, the error–tradeoff relation for error-free measurement of one observable is verified in our experiment. We also verify the error–tradeoff relations for nonzero errors and mixed state by introducing loss on one EPR beam. Our experimental results demonstrate that Heisenberg’s error–tradeoff relation is violated in some cases for a continuous-variable system, while the Ozawa’s and Branciard’s relations are valid.
npj Quantum Information 5:68 (2019) PDF
|

|
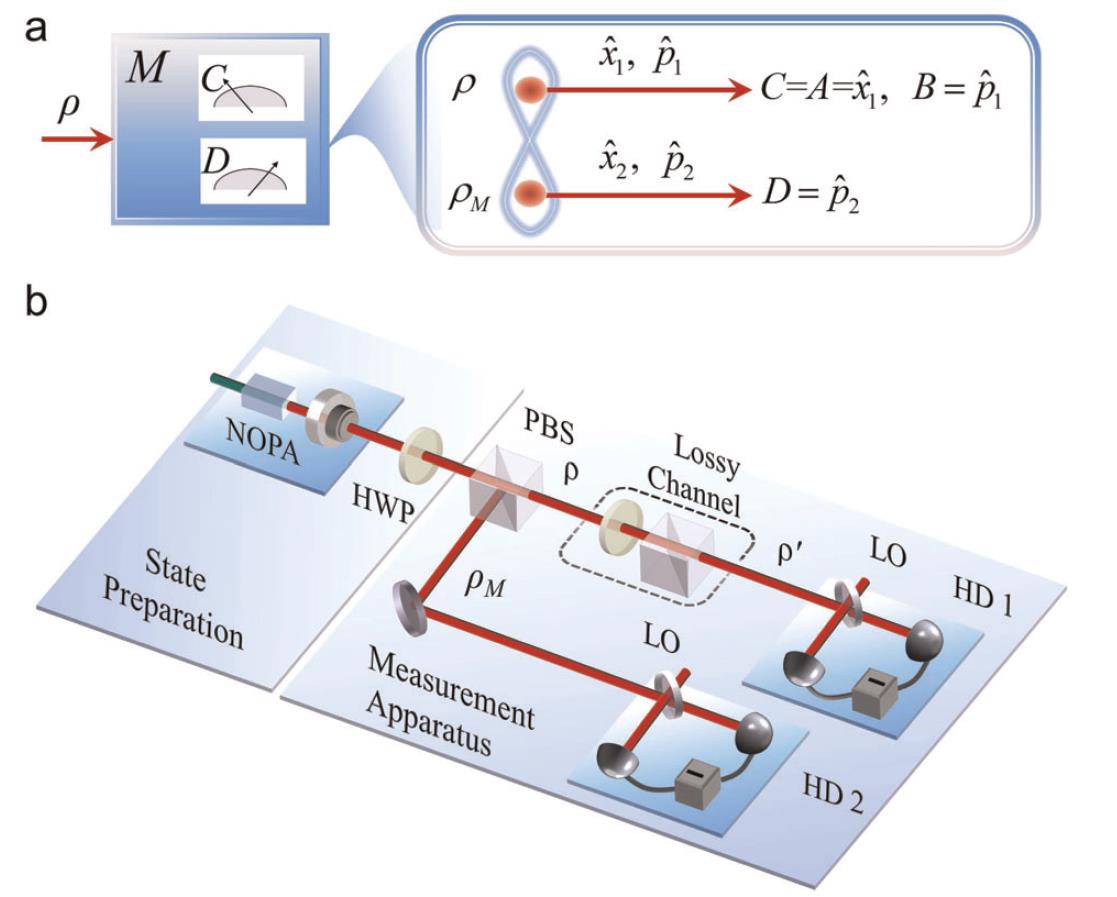
Characterizing the multipartite continuous-variable entanglement structure from squeezing coefficients and the Fisher information
Zhongzhong Qin, Manuel Gessner, Zhihong Ren, Xiaowei Deng, Dongmei Han, Weidong Li, Xiaolong Su, Augusto Smerzi, and Kunchi Peng
Understanding the distribution of quantum entanglement over many parties is a fundamental challenge of quantum physics and is of practical relevance for several applications in the field of quantum information. The Fisher information is widely used in quantum metrology since it is related to the quantum gain in metrology measurements. Here, we use methods from quantum metrology to microscopically characterize the entanglement structure of multimode continuous-variable states in all possible multi-partitions and in all reduced distributions. From experimentally measured covariance matrices of Gaussian states with 2, 3, and 4 photonic modes with controllable losses, we extract the metrological sensitivity as well as an upper separability bound for each partition. An entanglement witness is constructed by comparing the two quantities. Our analysis demonstrates the usefulness of these methods for continuous-variable systems and provides a detailed geometric understanding of the robustness of cluster-state entanglement under photon losses.
npj Quantum Information 5:3 (2019) PDF
|

|
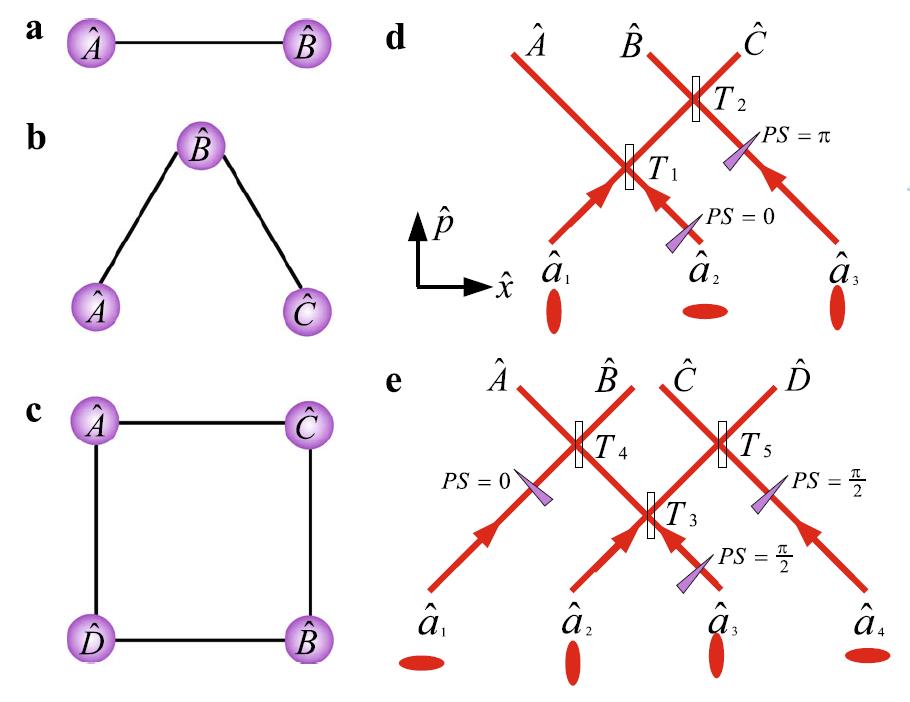
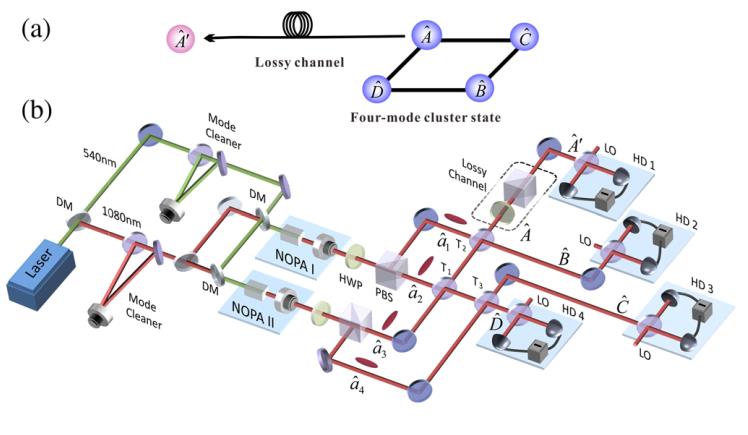
Demonstration of Monogamy Relations for Einstein-Podolsky-Rosen Steering in Gaussian Cluster States
Xiaowei Deng, Yu Xiang, Caixing Tian, Gerardo Adesso, Qiongyi He, Qihuang Gong, Xiaolong Su, Changde Xie, and Kunchi Peng
Understanding how quantum resources can be quantified and distributed over many parties has profound applications in quantum communication. As one of the most intriguing features of quantum mechanics, Einstein-Podolsky-Rosen (EPR) steering is a useful resource for secure quantum networks. By reconstructing the covariance matrix of a continuous variable four-mode square Gaussian cluster state subject to asymmetric loss, we quantify the amount of bipartite steering with a variable number of modes per party, and verify recently introduced monogamy relations for Gaussian steerability, which establish quantitative constraints on the security of information shared among different parties. We observe a very rich structure for the steering distribution, and demonstrate one-way EPR steering of the cluster state under Gaussian measurements, as well as one-to-multimode steering. Our experiment paves the way for exploiting EPR steering in Gaussian
cluster states as a valuable resource for multiparty quantum information tasks.
Phys. Rev. Lett. 118, 230501 (2017) PDF
|
|
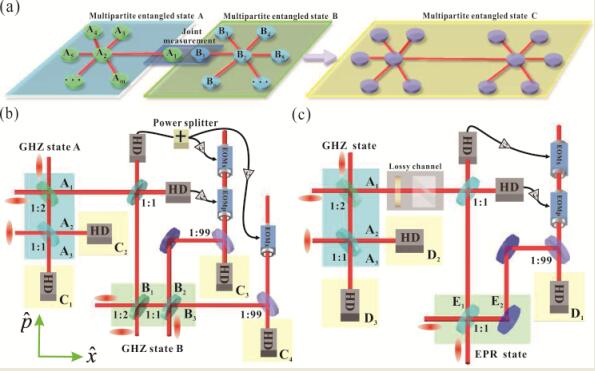
Quantum Entanglement Swapping between Two Multipartite Entangled States
Xiaolong Su, Caixing Tian, Xiaowei Deng, Qiang Li, Changde Xie, and Kunchi Peng
Quantum entanglement swapping is one of the most promising ways to realize the quantum connection among local quantum nodes. In this Letter, we present an experimental demonstration of the entanglement swapping between two independent multipartite entangled states, each of which involves a tripartite Greenberger-Horne-Zeilinger (GHZ) entangled state of an optical field. The entanglement swapping is implemented deterministically by means of a joint measurement on two optical modes coming from the two multipartite entangled states respectively and the classical feedforward of the measurement results. After entanglement swapping the two independent multipartite entangled states are merged into a large entangled state in which all unmeasured quantum modes are entangled. The entanglement swapping between a tripartite GHZ state and an Einstein-Podolsky-Rosen entangled state is also demonstrated and the dependence of the resultant entanglement on transmission loss is investigated. The presented experiment provides a feasible technical reference for constructing more complicated quantum networks.
Phys. Rev. Lett. 117, 240503 (2016) PDF
|
|
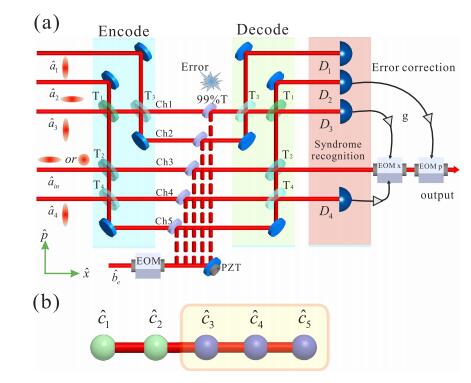
Five-wave-packet quantum error correction based on continuous-variable cluster entanglement
Shuhong Hao, Xiaolong Su, Caixing Tian,Changde Xie, and Kunchi Peng
Quantum error correction protects the quantum state against noise and decoherence in quantum communication and quantum computation, which enables one to perform fault -torrent quantum information processing. We experimentally demonstrate a quantum error correction scheme with a five-wave-packet code against a single stochastic error, the original theoretical model of which was firstly proposed by S. L. Braunstein and T. A. Walker. Five submodes of a continuous variable cluster entangled state of light are used for five encoding channels. Especially, in our encoding scheme the information of the input state is only distributed on three of the five channels and thus any error appearing in the remained two channels never affects the output state, i.e. the output quantum state is immune from the error in the two channels. The stochastic error on a single channel is corrected for both vacuum and squeezed input states and the achieved fidelities of the output states are beyond the corresponding classical limit.
Sci. Rep. 5, 15462 (2015) PDF
|